Slope Trick

Properties

สมบัติของฟังก์ชันที่ทำ Slope Trick ได้

1. เป็นฟังก์ชันต่อเนื่องบนจำนวนจริง
2. ฟังก์ชันนั้นสามารถแบ่งออกเป็นฟังก์ชันย่อย แล้วแต่ละฟังก์ชันย่อยเป็นฟังก์ชันเส้นตรงที่มีความชันเป็นจำนวนเต็ม
3. ฟังก์ชันนั้นต้องเป็น Convex Function (ฟังก์ชันที่เกิดจุดสูงสุดได้) หรือ Concave (ฟังก์ชันที่เกิดจุดต่ำสุดได้)

ข้อสังเกต ฟังก์ชันที่ทำ Slope Trick ได้มักจะมี $f_{k}(\infty) = -f_{k}(-\infty)$

Tutorial

ในการทำ Slope Trick จะใช้ Data Structure $[D]$ ในการเก็บจุดเปลี่ยนความชันของกราฟ โดยอาจใช้ std::multiset หรือ std::vector ในการเก็บได้

ค่าที่เก็บใน $[D]$ นั้นจะเป็นจุดเปลี่ยนความชันที่ทำให้ความชันเปลี่ยนไป $1$ เช่น

ในการเก็บเส้น $f_1(x)=|10-x|$ นั้นจะเก็บจุดตัดเป็น $[D] = \{10, 10\}$

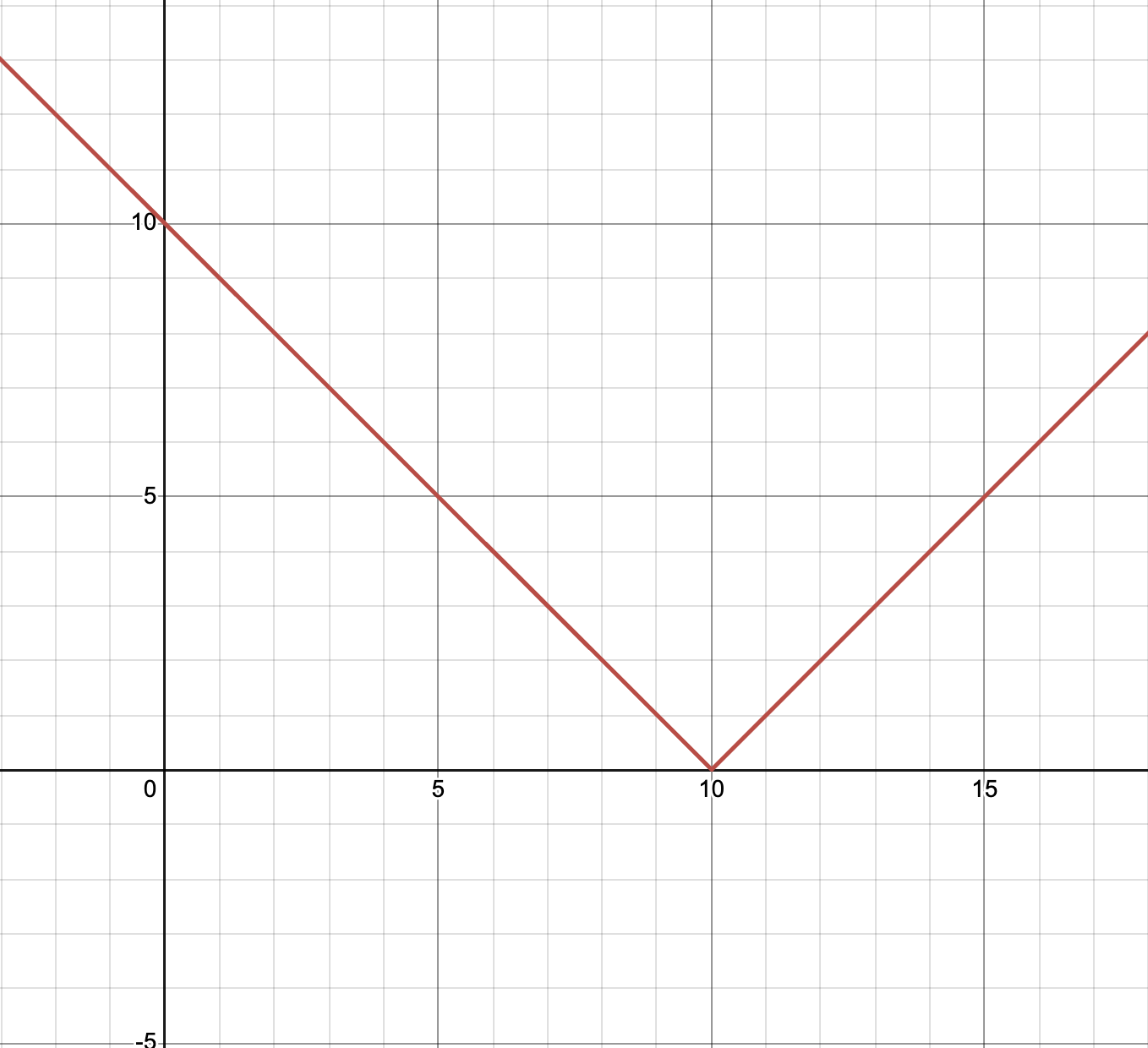
ถ้าเพิ่ม $f_2(x)=|8-x|$ เข้าไปอีกเส้นจะทำให้ $D=\{8,8,10,10\}$

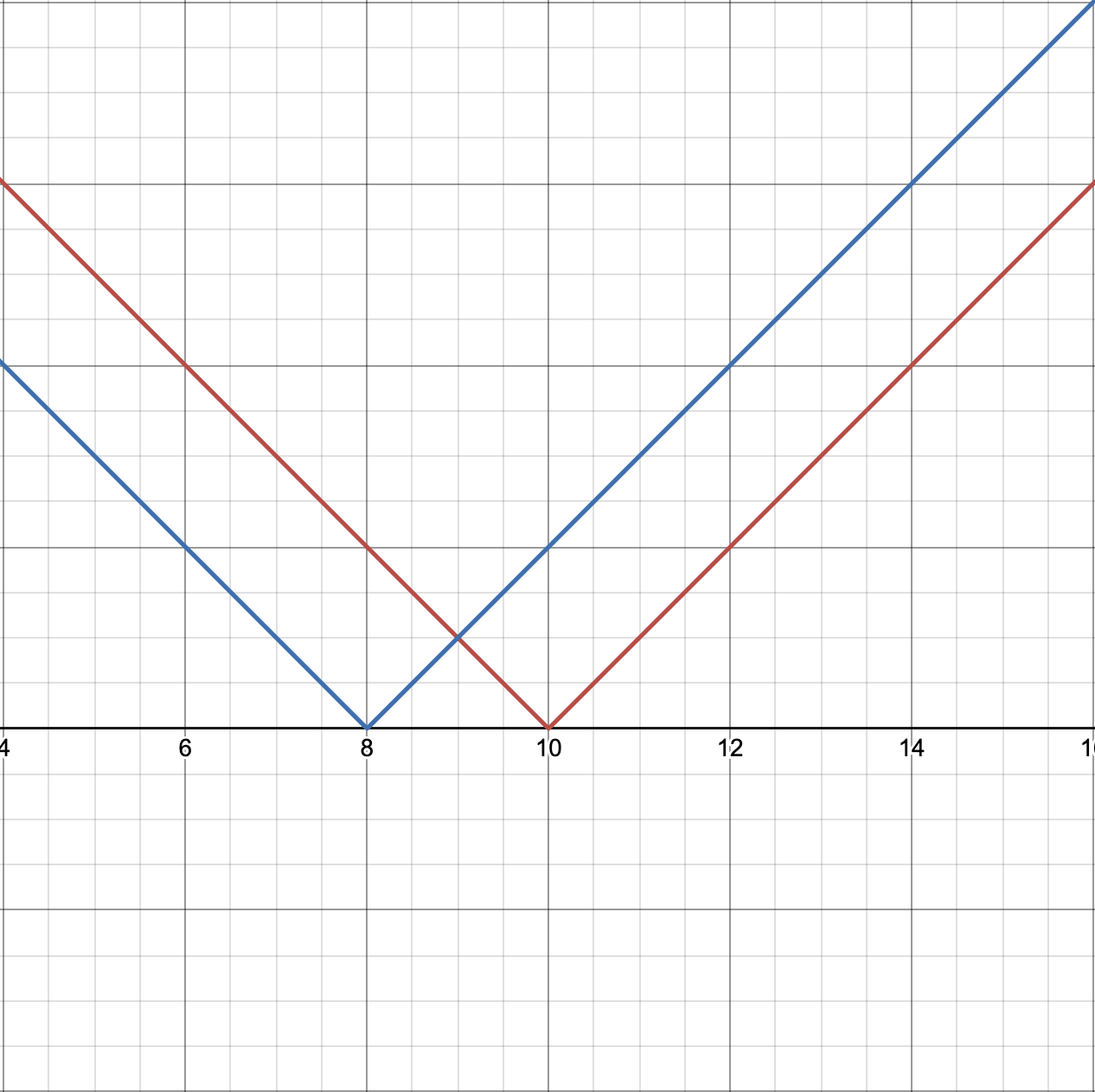
ฟังก์ชันของสองเส้นนี้รวมกันก็จะเป็น $s(x)=f_1(x)- f_2(x)=|10-x| - |8-x|$

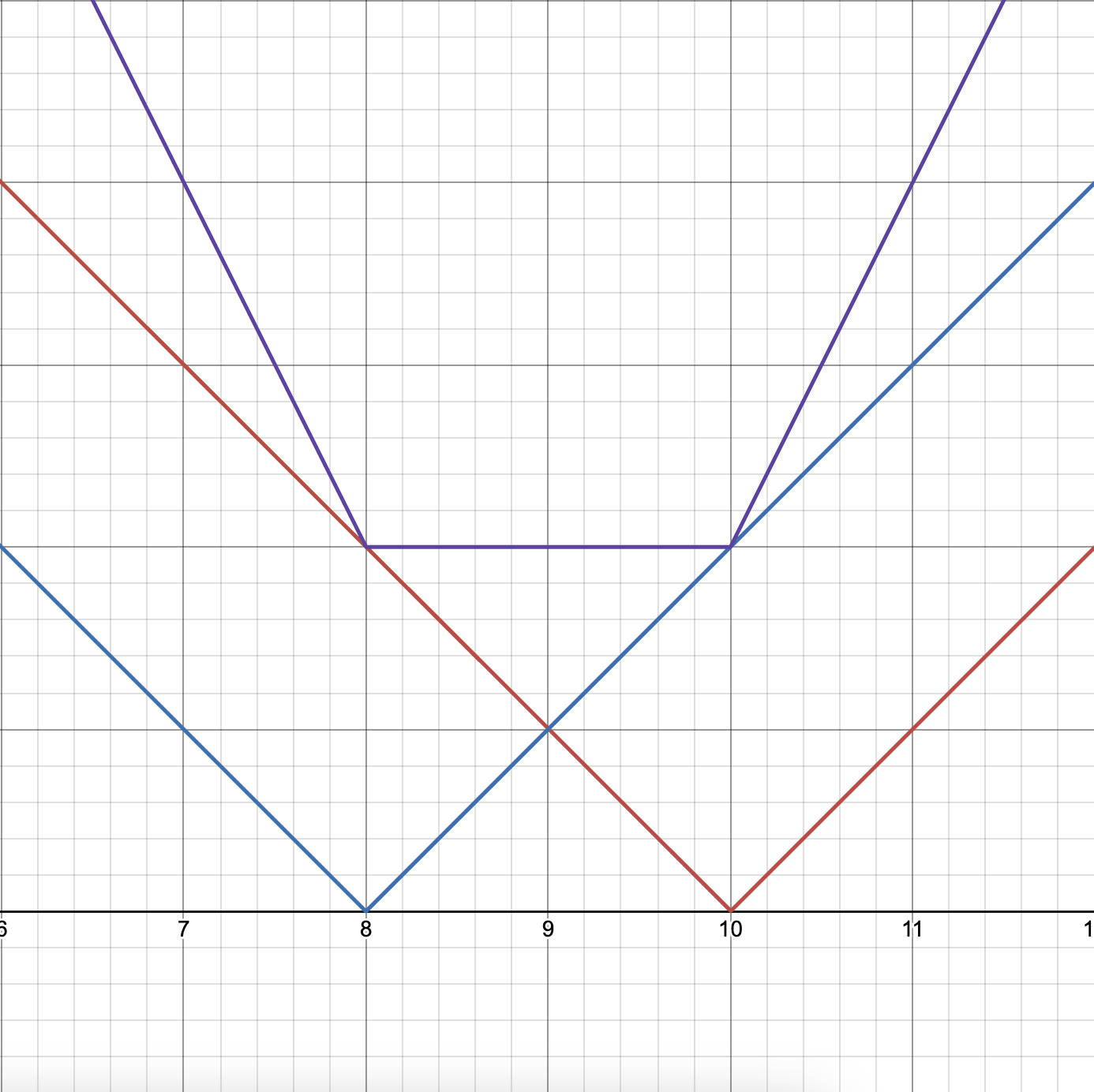
สังเกตว่า $s(x)$ (เส้นสีม่วง) จะมีจุดเปลี่ยนความชันที่ $8$ และ $10$ และแต่ละครั้งที่เปลี่ยนคือ $+2$ ทำให้ต้องเก็บจุดนั้น ๆ $2$ ครั้ง

ในบางครั้ง $[D]$ ก็อาจจะจำเป็นต้องเก็บ y-intercept (จุดตัดแกน y) และ slope (ความชัน) ร่วมด้วยได้

ในการรวมเส้น $2$ เส้นเข้าด้วยกัน y-intercept จะกลายเป็น $c_1 + c_2$ เมื่อ $c_i$ แทนจุดตัดแกน y ของเส้นที่ $i$ และรวมถึง slope ก็จะกลายเป็น $m_1 + m_2$ เมื่อ $m_i$ แทนความชันของเส้นที่ $i$ ด้วย

ปัญหาที่ใช้ Slope Trick ในการแก้

Median (การหาค่ามัธยฐาน)

โจทย์ กำหนดให้ $y = |A_1 - x| + |A_2 - x| + |A_3 - x| + \dots + |A_n - x|$ จงหาค่า $y$ ที่น้อยที่สุดที่เป็นไปได้

กำหนดให้ $f_i(x) := |A_1 - x| + |A_2 - x| + |A_3 - x| + \dots + |A_i - x|$ ที่มีค่าน้อยที่สุดเมื่อ $x \in \mathbb{Z}$
ดังนั้น $f_i(x) = |A_i - x| + f_{i-1}(x)$ หากกำหนดให้ $l_i = |A_i - x|$ แล้ว $f_i(x) = l_i + f_{i - 1}(x)$

และเมื่อนิยาม $f_n(x)$ แบบข้างต้นแล้วจะมีค่า $x$ ที่ดีที่สุดที่ทำให้ $(x, f(x))$ เป็นจุดต่ำสุดของ $y = f_n(x)$

ตัวอย่างการทำงาน

พิจารณา f_2(x)=|10-x|+|8-x|

สังเกตเส้น $l_1 = |10 - x|$ (เส้นสีแดง) และ $l_2 = |8 - x|$ (เส้นฟ้า) เมื่อรวมกันจะได้ $f_2(x)$ (เส้นสีม่วง) พอดี

จากนั้นเมื่อใส่ $l_3 = |9 - x|$ เข้าไปจะได้

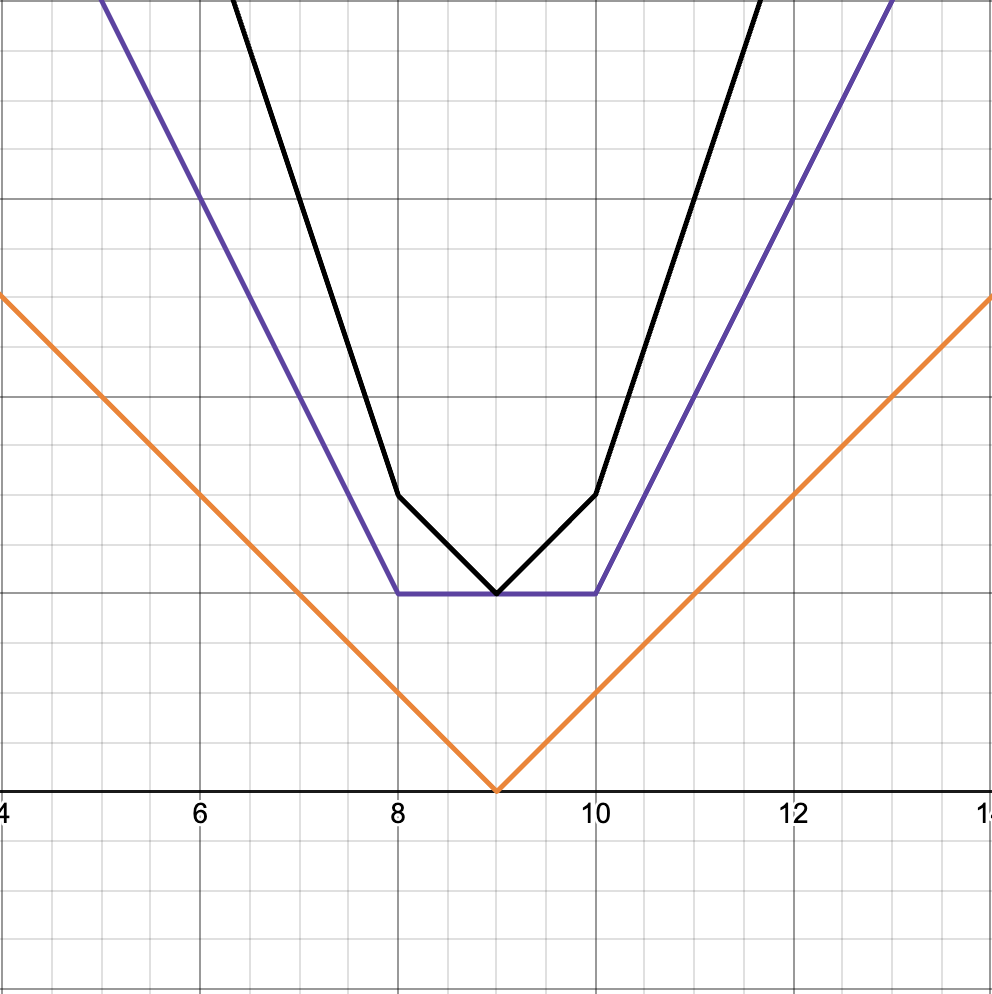
$l_3$ (เส้นสีเหลือง) เมื่อรวมเข้ากับ $f_2(x)$ จะได้ $f_3(x)$ (เส้นสีดำ) และเมื่อพิจารณาจุดที่ต่ำที่สุดของ $f_3(x)$ จะได้ค่ามัธยฐานของ $A_i$ ซึ่งมีค่าเท่ากับ $9$ และเมื่อแทน $x = 9$ ลงไปใน $f_3(x)$ จะได้ค่า $y$ ที่น้อยที่สุดที่เป็นไปได้ ซึ่งเท่ากับ $2$

NOI18_Safety

โจทย์(OJ.UZ) มีตึกอยู่ $N$ ตึก โดยตึกหมายเลข $i$ มีความสูง $A_{i}$ เมตร โดยตึกทั้งหมดนี้จะปลอดภัยก็ต่อเมื่อ $|A_{k} - A_{k + 1}| \le h$ สำหรับทุก $k = 1, 2, 3, \dots, N - 1$ ในการทำให้ตึกทุกตึกปลอดภัยนั้นสามารถทำ 2 operation ที่ทำได้ คือ

1. ลดความสูงของตึกหมายเลข $k$ ลง $1$ เมตร
2. เพิ่มความสูงของตึกหมายเลข $k$ อีก $1$ เมตร

ต้องการหาจำนวน operation ที่น้อยที่สุดที่ทำให้ตึกทั้ง $N$ ตึกนี้ปลอดภัย

ปัญหาย่อย $h = 0$

$f_i(x) :=$ จำนวน operation ที่น้อยที่สุดที่ทำให้ $A_i = x$ และ $A_1 = A_2 = \dots = A_{i}$
ดังนั้นจำนวน operation ในการทำให้ตึกที่ $i$ มีความสูง $x$ นั้นจะเท่ากับ $|A_{i} - x|$ ดังนั้น $f_{i}(x) = |A_{i} - x| + f_{i - 1}(x)$

ซึ่งสังเกตได้ว่าเหมือนกับปัญหา Median ด้านบน

ปัญหาเต็ม $h \le 10^9$

$f_i(x) :=$ จำนวน operation ที่น้อยที่สุดที่ทำให้ $A_i = x$ และ $|A_j - A_i + 1| \le h$ สำหรับ $1 \le j < i$

ดังนั้น $f_{i}(x) = |A_{i} - x| + \min_{x - h \le k \le x + h} \{f_{i-1}(k)\}$

$g_i(x) :=$ จำนวน operation ที่น้อยที่สุดที่ยังถูกเงื่อนไขเมื่อ $A_{i} = x$
$g_i(x) = \min_{x - h \le k \le x + h} \{f_{i-1}(k)\}$ ทำให้ $f_i(x) = |A_i - x| + g_{i - 1}(x)$

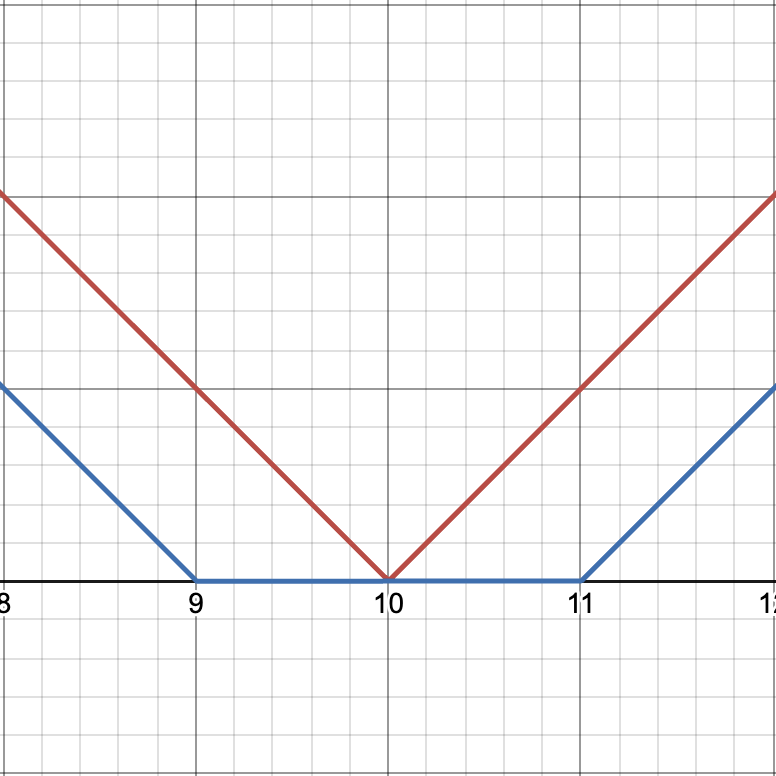
สังเกตว่า $f_{1}(x)$ เป็นเส้นสีแดงและ $g_{1}(x)$ เป็นเส้นสีฟ้า เนื่องจาก $g_{1}(x)$ เป็นจำนวน operation ที่น้อยที่สุดที่ยังถูกเงื่อนไขเมื่อ $A_{1} = x$ กล่าวคือเป็น $f_1(x)$ ที่ขยายไปทางซ้าย $-h$ และทางขวา $+h$

เมื่อใส่เส้นใหม่ไปเรื่อย ๆ ก็จะต้องขยายไปทางซ้าย $-h$ และขวา $+h$ ทุกครั้งทำให้ใน Data Structure ของเราจำเป็นต้องเก็บค่า lazy ไว้ด้วย โดยอาจใช้ lazy set มาช่วยได้

ในโจทย์ข้อนี้ไม่สามารถใช้ Lazy set เพียง 1 ตัวได้ เนื่องจากต้องการหาค่าที่อยู่ตรงกลางเนื่องจากกราฟเว้าลงมาจนตรงกลางของ Data Structure นั้นทำให้เกิดค่า $\min\{f_i(x)\}$ และเนื่องจากต้องการหาตรงกลางของ Data Structure และในการทำ lazy ค่า $h$ จึงสามารถใช้ Lazy set 2 ตัวเพื่อเก็บจุดเปลี่ยนความชันฝั่งซ้ายและขวา

ข้อสังเกต ในการใส่เส้นใหม่แต่ละครั้งทำให้อาจค่าของ $y$ ที่ต่ำที่สุดเปลี่ยนไปได้แต่ค่า $y$ ไม่สามารถลดลงได้เนื่องจากเพิ่มเส้นใหม่ลงไปเรื่อย ๆ และจำนวน operation ที่ใช้ก็จะเพิ่มขึ้นหรือเท่าเดิมไม่สามารถลดลงได้

Solution Code

Reference

• Slope Trick Tutorial
• Slope Trick Explained
• Slope Trick (IOI Training Thailand)